Simple Graphics Engine - Software Rasterizer banner

Simple Graphics Engine - Software Rasterizer

Created by: Jahaan
12 devlogs
61h 29m 16s

I created a simple software rasterizer in Java from scratch, the software rasterizer is able to load in obj files to create any model. The graphic engine contains rotation on all three axises, and also showcases lighting, and back-face culling, and triangle rasterization.

This project uses AI

Used Claude for learning to use git and helping to creating my first github release, and also to create the github workflow for the app to work for all OS

Demo Repository

README

Loading README...
Jahaan
Jahaan worked on Simple Graphics Engine - Software Rasterizer
1 day ago
0h 16m logged

Added new resources, and textures, the default will be a head model with skin texture.

Here is the new model, (just wanted to show this, no real change to the code has been made)

0
Jahaan
Jahaan worked on Simple Graphics Engine - Software Rasterizer
2 days ago
3h 40m logged

Implemented Textures onto any model, need to fix the perspective texture issue in the future.

TWO HOURS FOR DEBUGGING BECAUSE MY OBJ FILE WAS NOT IN THE CORRECT WINDING ORDER!!!!!!

0
Jahaan
Jahaan worked on Simple Graphics Engine - Software Rasterizer
2 days ago
1h 39m logged

Implemented camera rotation with quaternions. Added methods in my quaternion class, and camera class that integrate quaternion movement and rotation. Updated rasterizer class to handle the camera quaternion system.

0
Jahaan
Jahaan worked on Simple Graphics Engine - Software Rasterizer
3 days ago
3h 19m logged

Updates:

  • Added quaternion class for camera rotation

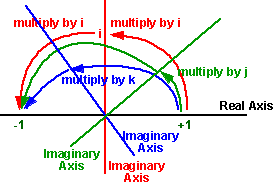
After making my camera rotation code through Euler Angles, I realized that real modeling engines and game engines don’t use Euler Angles fully as they have many disadvantages such as, computational heavy, gimbal, lock, etc. With research, I came across Quaternions, which are basically a 4-dimensional numerical system* (imp), with a real part (a) and an imaginary part (bi + cj + dk).

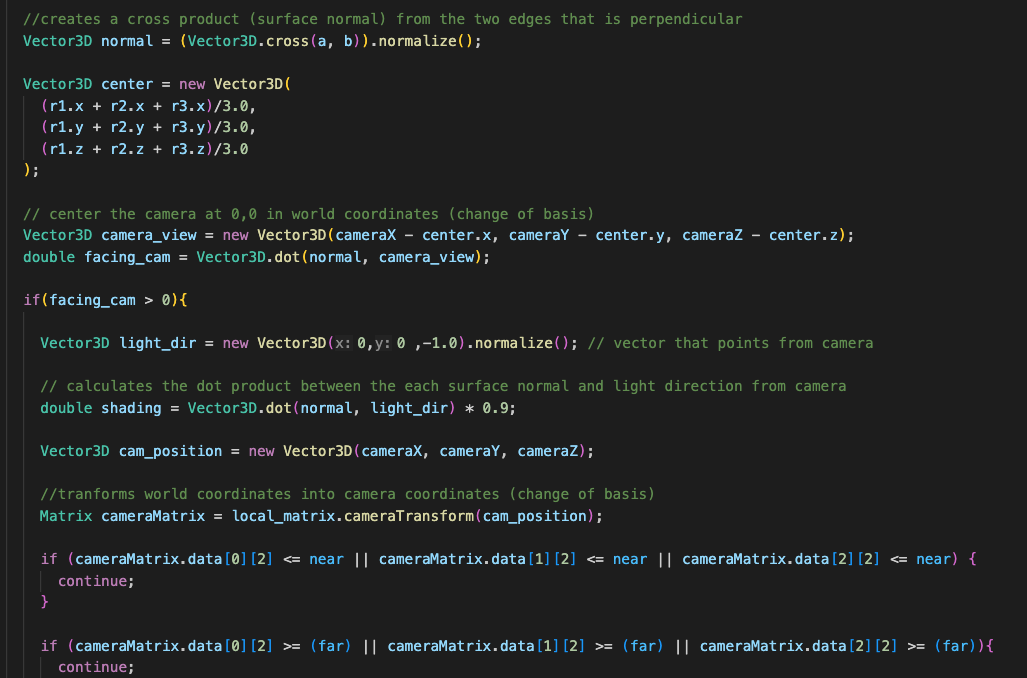
To explain briefly, just like how imaginary number i extends the numberline and shows rotation of a vector around an axis* (imp), quaternions entend that concept to bring that in 3d rotations (3-imaginary components which all represent orientation/position.) Just like rotation for the complex plane where we use exponents for faster and efficient math, (e^ix = cosx + isinx), we can extend this by taking the 3 components to represent 3D space, thus a quaternion rotation can be represent as: cos(x/2) + sin(x/2)(xi + yj + zk), where (xi + yj + zk) is one of the vector which we want to rotate around and cos(x/2) the amount we want to rotate. Multiplying two unit quaternions (like basis vectors) results in rotation from A to B, or B to A depending on order of multiplication. This can be calculated through cross product which gives us the perpendicular vector to the plane formed by A and B which is the same as axis, and the rotation amount can calculated as dot product (geometrically) between A and B. After knowing the point in quaternion number basis, we have to convert it into our 3D world, which is done through a change of basis, which I am still wrapping my head around.

P.S. the x/2 found in the rotation quaternion is there because due to the rules that define quaternions, after multiplying you find out that the end result is actually 2 times the rotation you wanted, thus the divide by 2.

Attachment
0
Jahaan
Jahaan worked on Simple Graphics Engine - Software Rasterizer
4 days ago
1h 50m logged

Update:

  • Cleaned code, by added methods/fucntions for conversion form NDC (normalized device coordinates ( -1 to 1)) into screen coordinates
  • Added Camera class to handle camera movement and camera rotation, instead of only being able to rotate the model
  • Seperated Vector3D and Vector4D into seperate classes, and added a couple of methods in both and Matrix classes

In this devlog, from my experience with all the OOP I learned along the way, I cleaned and fixed my code up so that its much better formatted and so that not everything is in the Rasterizer file. I also tried to implement camera rotation instead of just having model rotation, still currently doing that, but it different than rotating the mesh as that just a transformation, while moving the camera means to transform the model in the cameras basis/ coordinate system. Which is called Inverse Transformations, will learn that and keep updating. PEACE!!

Attachment
0
Jahaan
Jahaan worked on Simple Graphics Engine - Software Rasterizer
5 days ago
2h 49m logged

Update:

  • Cleaned up code by adding render function
  • Added and Learned about Depth Buffering
    • Create a class for DepthBuffer that creates the buffer
    • Implemented DepthBuffer into my LineDrawer and Rasterizer files
  • Also added clipping for near and far plane

In this devlog, I learned and added Depth Buffering. Depth Buffering otherwise known as Z-buffering removes any problem of rendering overlapping pixel, for example problems such as rendering farther objects on top of closer ones. It does this by comparing each pixel for z and draws the z that is closer (less) to the camera.

2

Comments

Jahaan
Jahaan 5 days ago

Also automated my github workflow, so that whenever i push any commit it automatically converts my code into executable files for windows and mac OS

Jahaan
Jahaan 5 days ago

For anyone that needs a good resource for Depth-Buffering and to know the Maths behind it and how to implement in code, here is a really good resource

https://www.scratchapixel.com/lessons/3d-basic-rendering/rasterization-practical-implementation/visibility-problem-depth-buffer-depth-interpolation.html

Jahaan
Jahaan worked on Simple Graphics Engine - Software Rasterizer
5 days ago
2h 23m logged

Updated:

  • Model Perspective
  • Near Clipping Plane
  • ClockWise triangle orientation

I finally fixed my perspective problem with my models, it was that for some weird reasons at particular rotations or orientations they would be way out of perspective. The issue of this problem was that i was calculating for Counter-Clockwise triangles, while I made my mesh with Clockwise orientation Meaning that when i calculate the cross-product what was suppose to be negative was actually positive adn vice-versa. Also added clipping by just saying that if the one of the points in the triangle are behind near plane, then dont include, I will soon switch to proper clipping which will calculate for each point instead.

P.S. Debugging this took more than 80% of the time, because I didn’t know why it wasnt working, and then found out that its because my thing had wrong orientation

Attachment
0
Jahaan
Jahaan worked on Simple Graphics Engine - Software Rasterizer
5 days ago
0h 20m logged

I made a yml file for my github workflow to automatically, convert the dmg file I made into a EXE file and bundle JRE file, with the help of Claude. I then pushed it onto my repo and updated my release. The demo should be working now, with a runnable app with exe file for Windows.

Attachment
1

Comments

Jahaan
Jahaan 5 days ago

Just to be clear, for this almost all the code was done through Claude (AI) as I didn’t have any experience, but I have learned and will do this by myself in the future

Jahaan
Jahaan worked on Simple Graphics Engine - Software Rasterizer
6 days ago
1h 17m logged

Oh boy, this was really rough, I spent like 2-3 hours just debugging. I ended up deleting my old repo and creating a new one just to clean and start anew with my new profound knowledge in using git and GitHub.

But i still messed up, as when i was creating my dmg file for my software rasterizer it just wouldn’t work. And when it worked, i had to make it so that the app could be received from every OS. I’m still in the middle of that, but I hope I can ship this tommorow and they can approve, so I can actually start adding features.

Attachment
0
Jahaan
Jahaan worked on Simple Graphics Engine - Software Rasterizer
7 days ago
1h 2m logged

After procastinating not using git, I spend a lot of time learning to use git on my laptop and getting used to pushing commits. Had a lot of trouble, but eventually got it to work.

I fixed up some file structure and then updated the ReadMe file to show my work properly, and be allow other people to test my program, and demo it.

I also fixed up a bit of the code, as it was messy and just overall cleaned up my entire project

Attachment
1

Comments

Jahaan
Jahaan 7 days ago

Also added my first ever release on github for other people to demo and use the software rasterizer! Hope you check it out, and have fun. I’ll keep updating it and adding bunch of stuff, with my end goal being to make it simulate wind tunnel testing for any model (fluid/aero dynamics)

Jahaan
Jahaan shipped Simple Graphics Engine - Software Rasterizer
8 days ago

Shipped this project!

Hours: 41.71
Cookies: đŸȘ 851
Multiplier: 20.41 cookies/hr

I made a Software Rasterizer in Java from scratch.

The rasterizer showcases perspective projection, rotation across all axes, translation, and lighting, and even interpolation which I haven’t demonstrated. But I really enjoyed making this project and obviously I have a lot to improve on especially adding depth buffering (removes those tiny lines you’ll see in the demo videos)

But I hope you’ll enjoy just as much, and vote for me! :) THANK YOUUUUUUUU

Jahaan
Jahaan worked on Simple Graphics Engine - Software Rasterizer
8 days ago
41h 42m logged

Created a Basic Software Rasterizer in Java:
The core of any graphic engine, or any graphics in general is the Graphics Pipeline:

  1. OBJ Loader and Model parser (Convert model into smaller triangles)
    Acquire the world coordinates/vertices (x,y,z) of the model. Given the coordinates we have to break them down into the simplest polygons— triangles. We load the models obj file into a custom Mesh parser, which sorts the vertices, and vertices into Triangles.

  2. Transformations (Rotation and Movement of Camera along axes)
    Once the model data is loaded, transformations are applied. These transformations are handled through matrix multiplication (which can be thought of as linear transformations) of rotation matrices, and transform matrix.

  3. Projection (3D –> 2D Conversion)
    After transforming the model, the next step is projecting 3D coordinates onto a 2D screen. I implemented a perspective projection matrix, which is just another type of linear transformation that simulates 3D perspective in 2D, by making things farther away look smaller, and vice-versa. This uses homogeneous coordinates (just add an extra dimension (w) ) which helps to add translation, as it is impossible to do translation with matrix multiplication.

  4. Perspective Divide (Normalization)
    Following projection, each vertex undergoes a perspective divide, where the x, y, and z components are divided by the w component. It gives true perspective and converts the coordinates into NDC (−1 to 1)

  5. Rasterize (What is Shown on screen)
    Finally, the normalized vertices are converted into screen space tiny pixels. I filled the triangles by calculating the cross-product of edges. For lighting, I took the dot product of surface-normals and view vector.

Thats just the gist of graphics programming, there is so much more to explore and add that i haven’t even touched. But overall I love this project, and I hope you also would find it cool and like it and maybe even try it out for yourself. :)

0